2020 Ph.D Thesis Defenses
Xian Dai
Title: Geodesic coordinates for the pressure metric at the Fuchsian locus
Thesis Advisor: Michael Wolf
Abstract: Higher Teichmu¨ller theory studies representations of a surface group into a general Lie group that arise as deformation of the classical Teichmu¨ller space. In this thesis, we focus on the Riemannian geometry for one family of Higher Teichmu¨ller spaces that are Hitchin components. We study a Riemannian metric, called the pressure metric, in the Hitchin component H3(S) of surface group representations into PSL(3, R) and prove that the Hitchin parametrization provides geodesic coordinates at the Fuchsian locus for the pressure metric in H3(S). The proof is a combination of thermodynamic formalism and Higgs bundle theory. We compute first derivatives of the pressure metric by using Thermodynamic formalism and subshifts of finite type. We then study flat connections from Hitchin’s equations and their parallel transports by invoking a gauge-theoretic formula. .
Hyunkyu Jun
Title: Cantor spectrum CMV matrices, Jacobi matrices and Schrodinger operators,
Thesis Advisor: David Damanik
Abstract: In this thesis, we consider CMV matrices, Jacobi matrices and Schrodinger operators with dynamically defined coefficients and potentials.
Charles Ouyang
Title: Degeneration of minimal surfaces in the bidisc
Thesis Advisor: Michael Wolf
Abstract: This thesis studies the degeneration of a particular class of minimal surfaces in the bidisc, describing both the limiting metric structure and geometry. Minimal surfaces inside symmetric spaces have been shown to be directly related to surface group representations into higher rank Lie groups by recent work of Labourie. Let S be a closed surface of genus g ≥ 2 and let ρ be a maximal PSL(2, R) × PSL(2, R) surface group representation. By a result of Schoen, there is a unique ρ-equivariant minimal surface Σ in H2 × H2. We study the induced metrics on these minimal surfaces and prove the limits are precisely mixed structures. In the second half of the thesis, we provide a geometric interpretation: the minimal surfaces Σ degenerate to the core of a product of two R-trees. As a consequence, we obtain a geometric compactification of the space of maximal representations of π1(S) into PSL(2, R) × PSL(2, R).
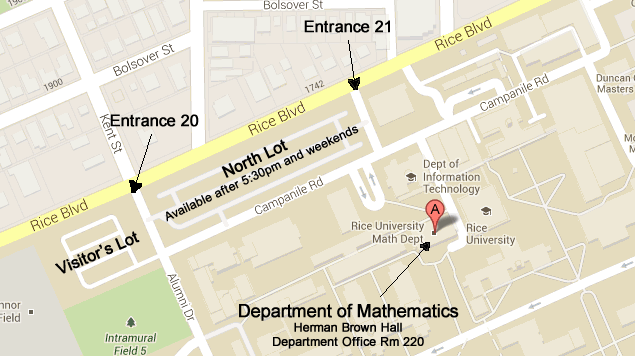
Contact Information
Tel (713) 348-4829
Mailing Address:
Rice University
Math Department -- MS 136
P.O. Box 1892
Houston, TX 77005-1892
Physical Address:
Rice University
Herman Brown Hall for Mathematical Sciences
6100 Main Street
Houston, TX 77005