2019 Ph.D Thesis Defenses
Alexis Johnson
Title: Brauer groups of Kummer surfaces arising from elliptic curves with complex multiplication
Thesis Advisor: Anthony Várilly-Alvarado
Abstract: The Brauer group of a variety often captures arithmetic information about the space. In this thesis, we study the Brauer group of a special kind of K3 surface, namely, a Kummer surface associated with a self-product of an elliptic curve over a number field with complex multiplication by a non-maximal order in an imaginary quadratic number field. Skorobogatov has conjectured that the Brauer group controls the existence of rational points on K3 surfaces. In practice, given a K3 surface, one often needs explicit descriptions of Brauer elements in order to study the behavior of rational points. The surfaces studied in this thesis have a geometrically rich structure that enables us to explicitly compute both the algebraic and transcendental Brauer groups over the rational numbers. Furthermore, over arbitrary number fields, we bound the transcendental Brauer group.
Miriam Kuzbary
Title: Link Concordance and Groups
Thesis Advisor: Shelly Harvey
Abstract: This work concerns the study of link concordance using groups, bothextracting concordance data from group theoretic invariants and deter-mining the properties of group structures on links modulo concordance.Milnor’s invariants are one of the more fundamental link concordance in-variants; they are thought of as higher order linking numbers and can becomputed using both Massey products (due to Turaev and Porter) andhigher order intersections (due to Cochran). In this thesis, we generalizeMilnor’s invariants to knots inside a closed, oriented 3-manifoldM. Wecall this the Dwyer number of a knot and show methods to compute itfor null-homologous knots inside a family of 3-manifolds with free funda-mental group. We further show Dwyer number provides the weight of thefirst non-vanishing Massey product in the knot complement in the am-bient manifold. Additionally, we prove the Dwyer number detects knotsK in M bounding smoothly embedded disks in specific 4-manifolds withboundary M which are not concordant to the unknot. This result fur-ther motivates our definition of a new link concordance group using theknotification construction of Ozsv`ath and Szab`o. Finally, we give a proofthat the string link concordance group modulo its pure braid subgroup isnon-abelian.
Sarah Seger
Title: Lower Order Solvability, Seifert Forms, and Blanchfield Forms of Links
Thesis Advisor: Shelly Harvey
Abstract: A slice knot was originally defined as a cross-section, or slice, of a sphere embedded in 4-dimensional space. Slice knots arise in the study of complex hypersurfaces, are related to the failure of the Whitney trick in 4 dimensions, and allow us to give the set of knots a group structure, but are difficult to detect. In 2003 Cochran, Orr, and Teichner introduced n-solvability of knots and links. Slice links are n-solvable for all n, and as n approaches infinity we may think of n-solvable links as successively finer approximations of slice links. For all integers n, there exist n-solvable knots that are not n.5-solvable, and yet all previous invariants cannot even distinguish slice knots from 1.5-solvable knots. Thus n-solvability gives a very rich set of invariants. Martin classifies 0-solvable links using Milnor’s invariants, however we show that Milnor’s invariants are insufficient to classify 0.5-solvable links. Since 0.5-solvable knots can be classified using Seifert matrices and Blanchfield forms, we define specific generalizations of these objects to links and look at their relationships to 0.5-solvability and to each other. We obtain a partial characterization of 0.5-solvable links.
Jianqiu Wu
Title: Smooth minimal transport networks and non-orientable minimal surfaces in S^3
Thesis Advisor: Robert Hardt
Abstract: In this paper we introduce a new optimal transport problem which involves roughly a finite system of simultaneous time-parametrized transport which (1) favors merging paths for efficiency at various times and (2) involves continuously differentiable transitions at the mergings (as with train tracks). We will describe suitable spaces of parametrized networks, topologies, and functionals, and then give an existence and regularity theory. Along the way we obtain necessary and sufficient optimality conditions applicable at times of various mergings. In the second part of this thesis we consider a problem of characterizing certain minimal surfaces in S^3. In particular, we are interested in whether a certain minimal Mobius band is the unique minimal nonorientable surface with boundary a great circle. As this problem is too hard to tackle directly, we studied a related problem in the bilipschitz space that is the boundary of the bi-cylinder D^2 * D^2.
Hang Yang
Title: On Singularity Formation of Monotone Flows
Thesis Advisor: Robert Hardt
Abstract: The well-posedness problem of Euler equations is one of the most intriguing yet difficult mathematical problems in fluids. The global existence of classical solutions of 2D Euler has been solved by Holder, Wolibner and the global existence of weak solutions by Yudovich. Yet in 3D, due to of quadratic non-linearity and non-locality, the global well-posedness of Euler’s equations remains unclear nowadays. In 2013, Hou-Luo investigated 3D Euler’s equations under the axisymmetric settings and observed numerical blow up on a ring of hyperbolic points on the boundary of the fluid domain. Their numerical simulation has shed important light on studying the evolution of vorticity of Euler equations. In this thesis, we will propose and discuss a few models of 3D Euler equations. In particular, with the modications to the original models, we are able to gain uniform control in the direction of the flows for the modi ed models, which will then create a scenario reminiscent of Hou-Luo’s numerical work. In these models, we show that solutions blow up in finite time for a wide range of initial data. Content of Chapter 2 includes a joint work with V. Hoang, M. Radosz and B. Orcan and content of Chapter 3 is a joint work with A. Kiselev. Both of these work are published and can be found in [1] and [2]. Content of Chapter 4 is being considered for publication.
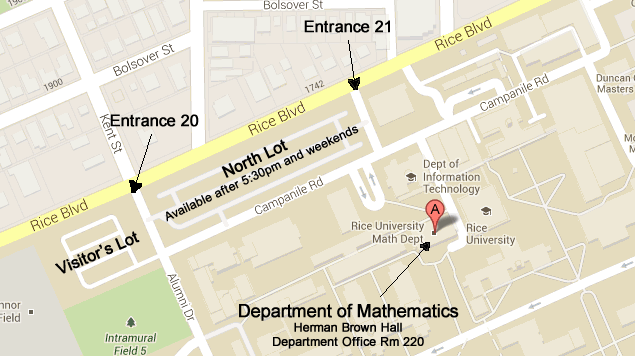
Contact Information
Tel (713) 348-4829
Mailing Address:
Rice University
Math Department -- MS 136
P.O. Box 1892
Houston, TX 77005-1892
Physical Address:
Rice University
Herman Brown Hall for Mathematical Sciences
6100 Main Street
Houston, TX 77005