2015 Ph.D Thesis Defenses
David Cohen
Title: The large scale geometry of strongly aperiodic subshifts of finite type
Date: Wednesday, March 18, 2015
Thesis Advisor: Andrew Putman
Abstract:
We discuss how the geometric properties of a group G constrain the possible dynamical properties enjoyed by subshifts of finite type on G.
Jacob Fillman
Title: Spectral Analysis of One-Dimensional Operators
Date: Tuesday, February 10, 2015
Thesis Advisor: David Damanik
Abstract:
We study the spectral analysis of one-dimensional operators, motivated by a desire to understand three phenomena: dynamical characteristics of quantum walks, the interplay between inverse and direct spectral problems for limit-periodic operators, and the fractal structure of the spectrum of the Thue-Morse Hamiltonian. Our first group of results comprises several general lower bounds on the spreading rates of wave packets defined by the iteration of a unitary operator on a separable Hilbert space. By using tools within the class of CMV matrices, we apply these general lower bounds to deduce quantitative lower bounds for the spreading of the time-homogeneous Fibonacci quantum walk on the integral lattice. Second, we construct several classes of limit-periodic operators with homogeneous Cantor spectrum, which connects problems from inverse and direct spectral analysis for such operators. Lastly, we precisely characterize the gap structure of the canonical periodic approximants to the Thue-Morse Hamiltonian.
Nikita Kozin
Title:Toric fibrations and models of universal torsors
Date: Monday, April 20, 2015
Thesis Advisor: Brendan Hassett
Abstract:
We study smooth projective threefolds fibered by toric surfaces over the projective line. We show that for certain families of degree 6 del Pezzo and quadric surface bundles the universal torsor corresponding to the generic fiber extends to a smooth model over the base. The model respects the action of the model of the Neron-Severi torus. For the latter we also compute the groups of principal homogeneous spaces.
Qiongling Li
Title: Hitchin components, Riemannian Metric and Asymptotics
Date: Tuesday, November 18, 2014
Thesis Advisor: Michael Wolf
Abstract:
The Higher Teichmueller spaces are certain deformation spaces arising from subsets of the space of representations of a surface group into general Lie groups, e.g., PSL(n,R), which share some of the properties of classical Teichmueller space. By the non-abelian Hodge theory, such representation spaces correspond to the space of Higgs bundles. We focus on two aspects on the Higher Teichmueller space: Riemannian geometry and dynamics. Firstly, we construct a new Riemannian metric on deformation space for PSL(3,R), and then prove Teichmueller space endowed with Weil-Petersson metric is totally geodesic in deformation space for PSL(3,R) with the new metric. Secondly, in a joint work with Brian Collier, we are able to obtain asymptotic behaviors of corresponding representations and related properties along certain families of Higgs bundles of rank n.
Diego Vela
Title: Infection by a String Link
Date: Monday, March 30, 2015
Thesis Advisor: Brendan Hassett
Abstract:
Satellite constructions on a knot can be thought of as taking some strands of a knot and then tying in another knot. Using satellite constructions one can construct many distinct isotopy classes of knots. Pushing this further one can construct distinct concordance classes of knots which preserve some algebraic invariants. Infection is a generalization of satellite operations which has been previously studies. An infection by a string link can be thought of as grabbing a knot at multiple locations and then tying in a link. Cochran, Friedl and Teichner showed that any algebraically slice knot is the result of infecting a slice knot by a string link\cite{CFT09}. In this paper we use the infection construction to show that there exist knots which arise from infections by $n$-component string links that cannot be obtained by $(n-1)$-component string links.
Contact Information
Tel (713) 348-4829
Mailing Address:
Rice University
Math Department -- MS 136
P.O. Box 1892
Houston, TX 77005-1892
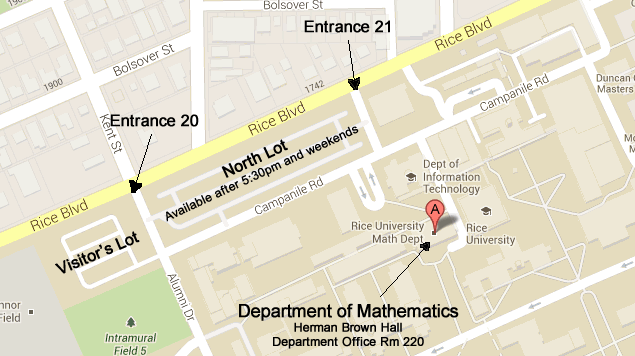
Physical Address:
Rice University
Herman Brown Hall for Mathematical Sciences
6100 Main Street
Houston, TX 77005