2012 Ph.D Thesis Defenses
Colin Carroll
Title: Minimizers of the vector-valued coarea formula
Date: Friday, April 6, 2012
Thesis Advisor: Robert Hardt
Abstract:
The vector-valued coarea formula provides a relationship between the integral of the Jacobian of a map from high dimensions down to low dimensions with the integral over the measure of the fibers of this map. We explore minimizers of this functional, proving existence using both a variational approach and an approach with currents. Additionally, we consider what properties these minimizers will have and provide examples. Finally, this problem is considered in metric spaces, where a third existence proof is given.
Christopher Davis
Title: First Order Signatures and Knot Concordance
Date: Wednesday, March 28, 2012
Thesis Advisor: Tim Cochran
Abstract:
Invariants of knots coming from twisted signatures have played a central role in the study of knot concordance. Unfortunately, except in the simplest of cases, these signature invariants have proven exceedingly difficult to compute. As a consequence, many knots which presumably can be detected by these invariants are not a well understood as they should be. We study a family of signature invariants of knots and show that they provide concordance information. Significantly, we provide a tractable means for computing these signatures. Once armed with these tools we use them first to study the knot concordance group generated by the twist knots which are of order 2 in the algebraic concordance group. With our computational tools we can show that with only finitely many exceptions, they form a linearly independent set in the concordance group. We go on to study a procedure given by Cochran-Harvey-Leidy which produces infinite rank subgroups of the knot concordance group which, in some sense are extremely subtle and difficult to detect. The construction they give has an inherent ambiguity due to the difficulty of computing some signature invariants. This ambiguity prevents their construction from yielding an actual linearly independent set. Using the tools we develop we make progress to removing this ambiguity from their procedure.
Bridget Franklin
Title: Obstructions to the Concordance of Satellite Knots
Date: Tuesday, March 27, 2012
Thesis Advisor: Tim Cochran
Abstract:
Formulas which derive common concordance invariants for satellite knots tend to lose information regarding the axis a of the satellite operation R(a,J). The Alexander polynomial, the Blanchfield linking form, and Casson-Gordon invariants all fail to distinguish concordance classes of satellites obtained by slightly varying the axis. By applying higher-order invariants and using filtrations of the knot concordance group, satellite concordance may be distinguished by determining which term of the derived series of the fundamental group of the knot complement the axes lie. There is less hope when the axes lie in the same term. We introduce new conditions to distinguish these latter classes by considering the axes in higher-order Alexander modules in three situations. In the first case, we find that R(a,J) and R(b,J) are non-concordant when a and b have distinct orders viewed as elements of the classical Alexander module of R. In the second, we show that R(a,J) and R(b,J) may be distinguished when the classical Blanchfield form of a with itself differs from that of b with itself. Ultimately, this allows us to find infinitely many concordance classes of R(-,J) whenever R has nontrivial Alexander polynomial. Finally, we find sufficient conditions to distinguish these satellites when the axes represent equivalent elements of the classical Alexander module by analyzing higher-order Alexander modules and localizations thereof.
Zheng Gan
Title: Spectral Properties of Limit-Periodic Schrodinger Operators
Thesis Advisor: David Damanik
Abstract:
We investigate spectral properties of limit-periodic Schrödinger operators in [cursive l] 2 ([Special characters omitted.] ). Our goal is to exhibit as rich a spectral picture as possible. We regard limit-periodic potentials as generated by continuous sampling along the orbits of a minimal translation of a procyclic group. This perspective was first proposed by Avila and further exploited by the author, which allows one to separate the base dynamics and the sampling function. Starting from this point of view, we conclude that all the spectral types (i.e. purely absolutely continuous, purely singular continuous, and pure point) can appear within the class of limit-periodic Schrödinger operators. We furthermore answer questions regarding how often a certain type of spectrum would occur and discuss the corresponding Lyapunov exponent. In the regime of pure point spectrum, we exhibit the first almost periodic examples that are uniformly localized across the hull and the spectrum.
Evelyn Lamb
Title: The Hopf differential and harmonic maps between branched hyperbolic structures
Date: Wednesday, December 21, 2011
Thesis Advisor: Michael Wolf
Abstract:
Given a surface of genus g with fundamental group π, a representation of π into PSL(2,R) is a homomorphism that assigns to each generator of π an element of P SL(2, R). The group P SL(2, R) acts on Hom(π, P SL(2, R)) by conjugation. Define therepresentationspaceRg tobethequotientspaceHom(π,PSL(2,R))\PSL(2,R). Associated to each representation ρ is a number e(ρ) called its Euler class. Goldman showed that the space Rg has components that can be indexed by Euler classes of rep- resentations, and that there is one component for each integer e satisfying |e| ≤ 2g−2. The two maximal components correspond to Teichmu ̈ller space, the space of isotopy classes of hyperbolic structures on a surface. Teichmu ̈ller space is known to be homeomorphic to a ball of dimension 6g − 6. The other components of Rg are not as well understood. The theory of harmonic maps between non-positively curved manifolds has been used to study Teichmu ̈ller space. Given a harmonic map between hyperbolic surfaces, there is an associated quadratic differential on the domain surface called the Hopf differential. Wolf, following Sampson, proved that via the Hopf differential, harmonic maps parametrize Teichmu ̈ller space. This thesis extends his work to the case of branched hyperbolic structures, which correspond to certain elements in non- maximal components of representation space. More precisely, a branched hyperbolic structure is a pair (M, σ|dz|2) where M is a compact surface of genus g and σ|dz|2 is a hyperbolic metric with integral order cone singularities at a finite number of points expressed in terms of a conformal parameter. Fix a base surface (M, σ|dz|2). For each target surface (M, ρ|dw|2) with the same number and orders of cone points as (M,σ|dz|2), there is a unique harmonic map w : (M,σ|dz|2) → (M,ρ|dw|2) homotopic to the identity that fixes the cone points of M pointwise. Thus we may define another map from the space of branched hyperbolic structures with the same number and orders of cone points to the space of meromorphic quadratic differentials on the base surface M. This map, Φ, takes the harmonic map w associated with a metric ρ|dw|2 to the Hopf differential of w. This thesis shows that the map Φ is injective.
Renee Laverdiere
Title: On geometry along grafting rays in Teichmuller space
Date: Friday, April 13, 2012
Thesis Advisor: Michael Wolf
Abstract:
In this work, we investigate the mid-range behavior of geometry along a grafting ray in Teichm\"{u}ller space. The main technique is to describe the hyperbolic metric $\sigma_{t}$ at a point along the grafting ray in terms of a conformal factor $g_{t}$ times the Thurston (grafted) metric and study solutions to the linearized Liouville equation. We give a formula that describes, at any point on a grafting ray, the change in length of a sum of distinguished curves in terms of the hyperbolic geometry at the point. We then make precise the idea that once the length of the grafting locus is small, local behavior of the geometry for grafting on a general manifold is like that of grafting on a cylinder. Finally, we prove that the sum of lengths of is eventually monotone decreasing along grafting rays.
Zhiyuan Li
Title: Density of rational points on K3 surfaces over function fields
Date: Wednesday, April 4, 2012
Thesis Advisor: Brendan Hassett
Abstract:
In this paper, we study sections of a Calabi-Yau threefold fibered over a curve by K3 surfaces. We show that there exist infinitely many isolated sections on certain K3 fibered Calabi-Yau threefolds and the subgroup of the N´eron-Severi group generated by these sections is not finitely generated. This also gives examples of K3 surfaces over the function field F of a complex curve with Zariski dense F-rational points, whose geometric models are Calabi-Yau. Furthermore, we also generalize our results to the cases of families of higher dimensional Calabi-Yau varieties with Calabi-Yau ambient spaces.
Fei Xu
Title: On the smooth linear section of the Grassmannian Gr(2, n)
Date: Tuesday, April 19, 2011
Thesis Advisor: Brendan Hassett
Abstract:
In this thesis, we will study the smooth linear section of the Grassmannian Gr(2, n). Explicitly, we give a criterion for the rationality of such linear section in terms of its codimension in the Plü ̈cker embedding in projective space. Moreover, to obtain a better understanding of the birational parametrization of these linear sections, we analyze their Hodge structures in the cases of even and odd codimensions. To be more precise, we provide numerous examples which suggest certain patterns of Hodge diamonds corresponding to even and odd cases and derive the proof of general patterns for codimension 3 smooth linear section of Gr(2, n) corresponding to odd and even n.
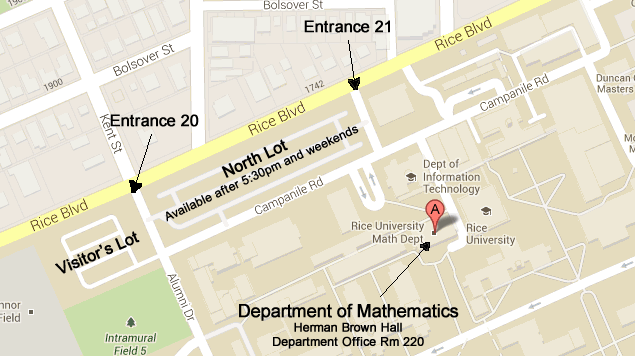
Contact Information
Tel (713) 348-4829
Mailing Address:
Rice University
Math Department -- MS 136
P.O. Box 1892
Houston, TX 77005-1892
Physical Address:
Rice University
Herman Brown Hall for Mathematical Sciences
6100 Main Street
Houston, TX 77005