Frank Jones - HB448 - fjones@rice.edu
Office Phone: 713-348-5266
Home Phone: 713-552-1822 (before 10:45 PM)
Office Hours: announced daily, or by appointment
Class Meets: MWF 11 AM HB 227
Book: I have written the text for the course, and although it is not yet published I have in my office bound copies for sale. The price of $34 is simply to cover the cost of photocopying and binding. You may pay me with cash or a personal check made out to Rice University. The chapters are available online in portable document format (PDF). They may be viewed on your computer if you have Adobe Acrobat Reader.
1. Euclidean Space
2. Differentiation
3. Higher order derivatives
4. Symmetric matrices
5. Manifolds
6. Implicit function theorem
7. Cross product
8. Volumes of parallelograms
9. Integration on Rn
10. Further investigation of integration
11. Integration on manifolds
12. Green's theorem
13. Stokes' theorem
14. Gauss' theorem
15. ∇ in other coordinates
A Highlight: Loxodrome (chapter 6)
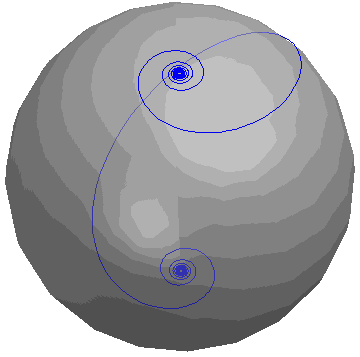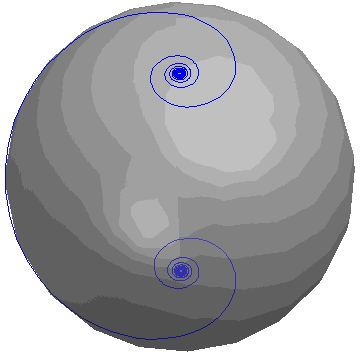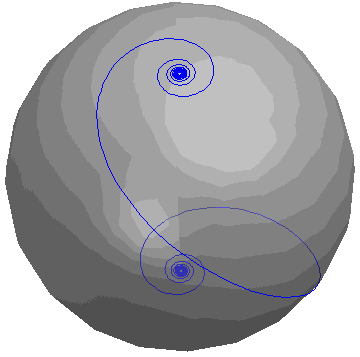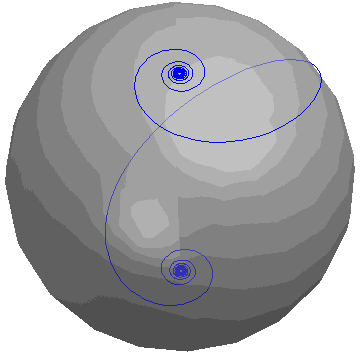
The blue line is a loxodrome, described parametrically by
x = cos (t) cos (atan (at))
y = sin (t) cos (atan (at))
z = -sin (atan (at)),
where a = 1. The loxodrome is being rotated about the z-axis.
Goal: To achieve a thorough understanding of vector calculus, including both problem solving and theoretical aspects. The orientation of the course is toward the problem aspects, though we go into great depth concerning the theory behind the computational skills that are developed.
This goal shows itself in that we present no “hard” proofs, though we do present “hard” theorems. This means that you are expected to understand these theorems as to their hypotheses and conclusions, but not to understand or even see their proofs. However, “easy” theorems are discussed throughout the course, and you are expected to understand their proofs completely. For example, it is a hard theorem that a continuous real-valued function defined on a closed interval of the real numbers attains its maximum value. But it is an easy theorem that if that maximum value is taken at an interior point of the interval and if the function is differentiable there, then its derivative equals zero at that point.
You also will learn to grasp quite a large number of important definitions. For instance, one of the most important definitions, the differentiability of a function of several real variables, is utterly important, and you’ll confront it right away in Chapter 2.
Since we are discussing vector calculus throughout the year, and a great deal of what we do takes place in n-dimensional Euclidean space, a large amount of basic linear algebra will need to be developed as we go along. In fact, a high point of the course is the “principal axis theorem” of Chapter 4, a theorem which is completely about linear algebra. We also shall need to discuss determinants in some detail in Chapter 3.
The first semester is mainly restricted to “differential” calculus, and the second semester treats “integral” calculus.
The combination MATH 321/322, Introduction to Analysis, treats in great detail the proofs of the hard theorems alluded to above.
Prerequisites: A good one-year course in single-variable calculus, and especially a genuine love for mathematics.
Exams: There will be a take-home final examination each semester.
Homework: This will be assigned daily. The HW is not pledged. I definitely encourage you to work together on the assignments, though each student is responsible for the final preparation of his or her own HW submission.
Final exam: There will be a take-home final exam, also open book.
Grading: I shall take all aspects into consideration, especially your progress during the semester.
